Volume of Rectangle Formula How to Calculate it Easily
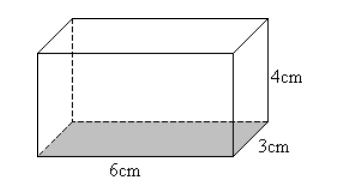
The volume of a rectangular prism is an important concept in geometry and is often encountered when dealing with three-dimensional objects. Understanding the formula for calculating the volume of a rectangle can be beneficial in various fields such as architecture, engineering, and construction. In this article, we will explore the intricacies of finding the volume of a rectangular prism and provide detailed explanations along with practical examples.
Formula for a Rectangular Prism’s Volume
The volume of a rectangular prism is calculated by multiplying its length, width, and height. The formula for finding the volume can be expressed as:
Volume = Length × Width × Height
This straightforward formula allows us to determine the amount of space occupied by a rectangular prism in cubic units.
For Example:
Let’s consider a rectangular prism with a length of 5 units, a width of 3 units, and a height of 2 units. To find its volume, we apply the formula:
Volume = 5 × 3 × 2 = 30 cubic units
Hence, the volume of this rectangular prism is 30 cubic units.

What other formulas exist for a rectangular prism’s volume?
The volume of a rectangular prism formula remains unchanged regardless of whether the dimensions are given as whole numbers or fractions. However, depending on the information provided, different approaches can be employed to calculate the volume.
For Example:
- Whole Numbers: Suppose we have a rectangular prism with a length of 8 units, a width of 2 units, and a height of 6 units. Using the volume formula, we can determine the volume as follows:
Volume = 8 × 2 × 6 = 96 cubic units
- Fractions: Consider a rectangular prism with a length of 4/5 units, a width of 3/4 units, and a height of 2/3 units. To find its volume, we apply the formula by multiplying the fractions:
Volume = (4/5) × (3/4) × (2/3) = 8/15 cubic units
Therefore, it is evident that the volume of a rectangular prism can be calculated using the same formula, irrespective of the type of numbers involved.

How can you figure out a rectangle’s volume?
To calculate the volume of a rectangle, it is crucial to measure or know the values of its length, width, and height. With these measurements at hand, the volume can be obtained using the formula mentioned earlier.
For Example:
Let’s consider a rectangle with a length of 10 units, a width of 6 units, and a height of 4 units. Applying the volume formula, we can calculate its volume as follows:
Volume = 10 × 6 × 4 = 240 cubic units
Thus, the volume of the given rectangle is 240 cubic units.
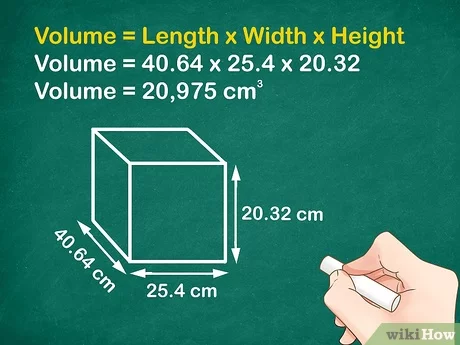
How can the volume of a rectangular prism be determined?
To find the volume of a rectangular prism, it is necessary to follow these steps:
- Measure or obtain the values of the length, width, and height of the rectangular prism.
- Apply the volume formula: Volume = Length × Width × Height.
- Substitute the respective values into the formula.
- Perform the multiplication to obtain the volume in cubic units.
For Example:
Suppose we have a rectangular prism with a length of 7 units, a width of 5 units, and a height of 3 units. By substituting these values into the volume formula, we can determine the volume as follows:
Volume = 7 × 5 × 3 = 105 cubic units
Hence, the volume of the given rectangular prism is 105 cubic units.
Practice Questions Regarding Rectangular Prism Volume
- Calculate the volume of a rectangular prism with a length of 9 units, a width of 4 units, and a height of 6 units.
- A rectangular prism has a length of 12 units, a width of 5 units, and a volume of 360 cubic units. Determine its height.
- Find the volume of a rectangular prism with a length of 10 units, a width of 8 units, and a height of 2 units.
FAQs on Volume of Rectangle Formula
1. What is a rectangular prism’s volume?
The volume of a rectangular prism refers to the amount of space enclosed by the prism in three dimensions. It represents the total capacity or size of the object and is measured in cubic units.
2. What is the formula for a rectangular prism’s volume?
The formula for calculating the volume of a rectangular prism is obtained by multiplying its length, width, and height:
Volume = Length × Width × Height
3. How to find the volume of a rectangular prism?
To find the volume of a rectangular prism, follow these steps:
- Measure or obtain the values of the length, width, and height of the prism.
- Use the formula: Volume = Length × Width × Height.
- Substitute the respective values into the formula.
- Perform the multiplication to obtain the volume in cubic units.
4. How to find the height of a rectangular prism when the volume of a rectangular prism is given?
If the volume of a rectangular prism is given, and you want to find the height, you can rearrange the volume formula. Divide both sides of the equation by the product of the length and width:
Height = Volume / (Length × Width)
Substitute the known values of volume, length, and width into the formula to calculate the height.
5. What happens to the volume of a rectangular prism if its height is doubled?
If the height of a rectangular prism is doubled while keeping the length and width unchanged, the volume will also be doubled. This is because the volume of a rectangular prism is directly proportional to its height. Increasing the height proportionally increases the amount of space enclosed by the prism.
6. What happens to the volume of a rectangular prism if the length is doubled and the height is reduced to one-half?
If the length of a rectangular prism is doubled while the height is reduced to one-half, the volume remains the same. This is because the change in length is compensated by the inverse change in height, resulting in an equivalent volume. The width is unaffected in this scenario.
7. What happens to the volume of a rectangular prism if the length, width, and height of the prism are doubled?
If all dimensions of a rectangular prism (length, width, and height) are doubled simultaneously, the volume will increase by a factor of 8. This is because volume is calculated by multiplying the three dimensions together. Doubling each dimension results in multiplying the volume by 2 × 2 × 2 = 8.
8. How to find the volume of a rectangular prism with fractions?
When dealing with fractions, multiply the numerators to get the numerator of the result and multiply the denominators to obtain the denominator of the result. Apply the same logic to find the volume of a rectangular prism with fractions:
Volume = (Length fraction) × (Width fraction) × (Height fraction)
Multiply the numerators of the fractions to obtain the numerator of the result and multiply the denominators of the fractions to obtain the denominator of the result. Simplify if necessary.
Conclusion
Understanding the volume of a rectangular prism formula is essential for various applications involving three-dimensional objects. By knowing the length, width, and height, you can easily calculate the volume using the formula Volume = Length × Width × Height. We explored different scenarios, including whole numbers and fractions, and examined how changes in dimensions affect the volume. Remember to carefully measure or obtain the required values and follow the steps outlined to find the volume accurately. Mastery of this formula will empower you to solve practical problems in fields such as construction, architecture, and engineering.





